Protect Your Family from Big Tech’s Influence
More Than 2 Million Parents Love Mobicip
Featured on








-
Limit
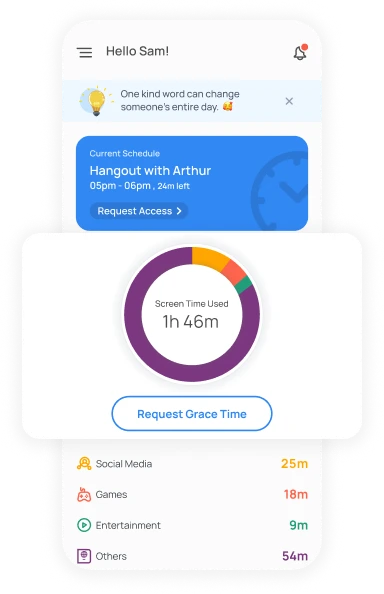
Effectively manage screen addiction with healthy limits
Set daily/weekly screen time limits, set app limits for using specific apps, and customize schedules to organize screen time and app usage at different times of the day/week.

-
Protect
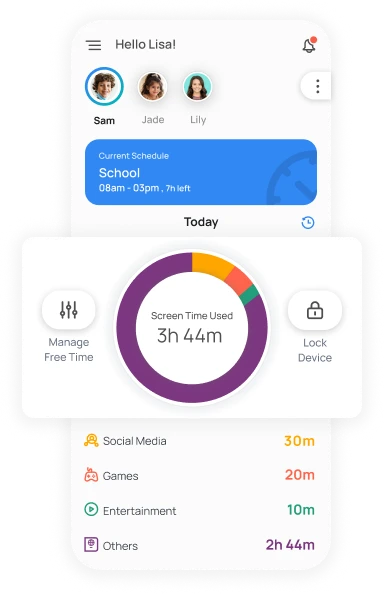
AI-based parental control that fights Big Tech
Filter inappropriate content on the internet, block apps, distracting games and provide an SOS button for your kids to instantly send a digital call for help in case of emergency.

-
Monitor
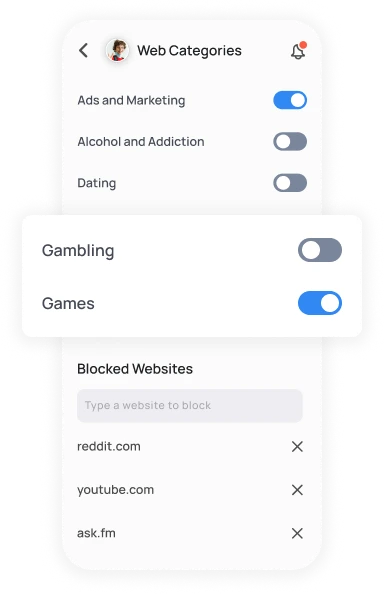
Monitor online habits & intervene when alerted
Monitor conversations on the top 3 social media apps, create geo-fences, locate your family instantly, and get reports on how your kids spend their time online.


-
Collaborate
Collaborate with your children and parenting partners
Set mutually acceptable goals & rewards to motivate your children, get a curated list of expert resources and share digital parenting responsibilities with guardians.